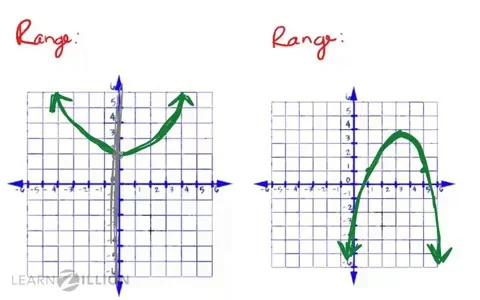
Domain And Range From The Graph Of A Continuous Function Parabola
Domain And Range From The Graph Of A Continuous Function Youtube
Domain Range Of Linear Functions Using Graphs Summer School Math Activities Math Tutoring Activities Maths Activities Middle School
Piecewise Continuous And Noncontinuous Precalculus Algebra Function
Pin On High School Math Ideas
Activity Domain And Range 2 Algebra 2 Ti Math Nspired Algebra Algebra Ii Math
Analyze Functions Domain Range Max Min Increasing Decreasing Teaching Algebra Algebra Resources Math Interactive Notebook
Two endpoints graph covers all 7 x 5 notice that this graph has two endpoints so the graph starts and stops and the domain covers all x values.
Domain and range from the graph of a continuous function parabola. When looking at a graph the domain is all the values of the graph from left to right. One of these is the domain of a parabola which indicates all possible values of x included at some point along the parabola s arms. The vertex of a parabola is an extreme point of a quadratic function and in general it is known as maximum or minimum of a parabola.
Another way to identify the domain and range of functions is by using graphs. Another way to identify the domain and range of functions is by using graphs. If the function you re graphing is an even ordered function you re going to have a parabola of some type.
The domain is all x values or inputs of a function and the range is all y values or outputs of a function. For a function to be continuous at a point the function must exist at the point and any small change in x produces only a small change in f x. Because the domain refers to the set of possible input values the domain of a graph consists of all the input values shown on the x axis the range is the set of possible output values which are shown on the y axis keep in mind that if the graph continues beyond the portion of the graph we can see the domain and.
We observe that a small change in x near x 1 gives a very large change in the value of the function. The range is the set of possible output values which are shown on the latex y latex axis. This article explains step by step how to find the domain and range of a parabola with any orientation.
Because the domain refers to the set of possible input values the domain of a graph consists of all the input values shown on the latex x latex axis. When working with a parabola there are a few details that are useful to calculate. The range is all the values of the graph from down to up.
Range y y 0 25 to have better understanding on domain and range of a quadratic function let us look at the graph of the quadratic function y x 2 5x 6. It is the point where the graph intersects its axis of symmetry. The graph of a continuous function can be drawn without lifting the pencil from the paper.
Domain Range And End Behavior Of Functions Task Cards Task Cards Behavior Set Notation
Domain And Range Free Math Activity Math Lessons Free Math
How To Get The Domain And Range From The Graph Of A Function Krista King Math Online Math Tutor
Determine If A Function Is Discrete Or Continuous By Analyzing The Domain Learnzillion Continuity Rational Function Analyze
Determine The Domain And Range Of A Parabola Looking At The Graph Learnzillion
Parabolas Domain And Range Youtube
Students Will Create A Roller Coaster That Demonstrates Their Knowledge And Understanding Of The Following Skills Graph Functions Math Teaching Algebra Math
Domain And Range Graph Worksheet With Answers Luxury Collection Of Domain Range Worksheet In 2020 Graphing Worksheets Dr Note For Work
Quadratics Quiz Parts Of The Graph Factoring Quadratics Graphing Powerpoint Format
Functions And Relations Review Or Asessment Identifying Functions Map Diagram Relatable
Continuous And Discrete Sorting Cards Sorting Cards Sorting Activities Cards
Relations Functions And Domain And Range 7th 10th Grade Worksheet Worksheets Graphing Functions Algebra
Parent Functions Graphic Organizers Algebra Graphic Organizers Teaching Algebra
